CSS3 transform 中的Matrix(矩阵)

https://www.zhangxinxu.com/wordpress/2012/06/css3-transform-matrix-%e7%9f%a9%e9%98%b5/

什么是矩阵？

矩阵可以理解为方阵，只不过，平时方阵里面站的是人，矩阵中是数值。

↓

$$
\begin{bmatrix}
1 & 4 & 5\newline
10 & 3 & 6\newline
9 & 10 & 1
\end{bmatrix}
$$

CSS3中的矩阵

CSS3中的矩阵指的是一个方法，书写为matrix()和matrix3d(),前者是元素2D平面的移动变换(transform),后者则是3D变换，2D变换举证为3×3，如上图中的矩阵示意图；3D变换则是4×4的矩阵。
现在，先看一下transform属性：

.trans_skew { transform: skew(35deg); }
.trans_scale { transform:scale(1, 0.5); }
.trans_rotate { transform:rotate(45deg); }
.trans_translate { transform:translate(10px, 20px); }

• skew——斜拉
• scale——缩放
• rotate——旋转
• translate——位移

为什么transform: rotate(45deg)会让元素旋转45°呢？这背后运作的机理是什么呢？
下面这张图可以结束上面的疑问：

无论是旋转还是倾斜，本质上都是应用的matrix()方法实现的（修改matrix()方法固定几个值），只是类似于transform:rotate()这种表现形式，我们更容易理解、记忆与上手。

矩阵应用的场景

虽然题目写的是transform中的Matrix,实际上，在CSS3记忆HTML5的世界里，这玩意还是涉猎很广的，比如svg和Canvas。

transform与坐标系统

用过transform旋转的人可以发现了，其默认是绕着中心点旋转的，而这个中心点就是transform-origin属性对应的点，也是所有矩阵计算的一个重要的依据点：

当我们通过transform-origin属性进行设置的时候，矩阵相关计算也随之发生改变，反应到实际图形效果上就是，旋转倾斜的中心点变了。
举例来说，如果我们设置：

-webkit-transform-origin: bottom left;

则，中心店就是左下角的位置。于是动画（例如图片收缩）就是基于图片的左下角这一点：

再举个例子，我们如果这样设置：

transform-origin: 50 px 70px;

则，中心点位置有中间移动到了举例左侧50像素，顶部70像素的地方（如下图），而此时的（30，30）的坐标为白点所示的位置（这个位置后面会用到）。

重点（平移）

CSS3transform的matrix()方法写法如下：

transform: matrix(a,b,c,d,e,f);

实际上，这6个参数，对应的举证就是：
$$\begin{bmatrix}
1 & 4 & 5\newline
10 & 3 & 6\newline
9 & 10 & 1
\end{bmatrix}$$

$$\begin{bmatrix}
a & c & e\newline
b & d & f\newline
0 & 0 & 1
\end{bmatrix}$$

注意书写方向是竖着的，
上面提过，矩阵可以想象成古代的士兵方阵，要让其发生变化，只有与另外一个士兵火拼就可以了，即使这是个小阵。
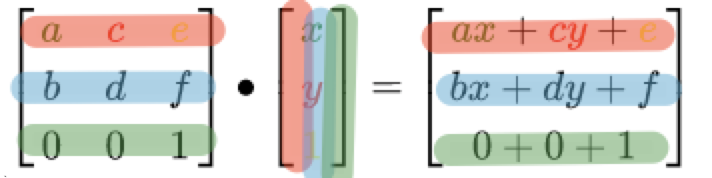
反应在这里就是如下转换公式：
$\begin{bmatrix}
a & c & e\newline
b & d & f\newline
0 & 0 & 1
\end{bmatrix} \bullet
\begin{bmatrix}
x \newline
y \newline
1
\end{bmatrix} =
\begin{bmatrix}
ax + cy + e \newline
bx + dy + f \newline
0 + 0 + 1
\end{bmatrix}$
其中，x，y标识转换元素的所有坐标（变量），后面就是大学时候线性代数的知识：

很简单，3×3矩阵每一行的第一个值与后面1×3的第一个值相乘，第二个值与第二个相乘，第三个与第三个相乘，然后相加，如下面同色标注

那么ax+cy+e表示什么意思呢？
答：ax+cy+e为变换后的水平坐标，bx+dy+f为变换后的垂直坐标。

下面举例说明，加深举证参数如下：

transform: matrix(1, 0, 0, 1, 30, 30);/** a=1 b=0 c=0 d=1 e=30 f=30 */

现在我们根据这个矩阵偏移元素的中心点，假设为(0,0)点，即：x=0,y=0。
于是，变换后x坐标就是ax + cy + e = 1×0 + 0×0 + 30，y坐标就是bx + dy + f = 0×0 + 1×0 + 30 = 30。
于是，中心点坐标(0,0)变成了(30,30)。对照上面有个(30,30)的白点图，好好想象下，原来(0,0)的位置，移动到了白点的(30,30)处，同理：(10,10)点变成(40,40),(11,11)点变成了(41,41),(x,y)变成了(x + 30, y + 30) ,由此可以了解到，该语句的作用就是向右移动30像素，向下移动30像素。
实际上transform: matrix(1, 0, 0, 1, 30 , 30)就等同于transform: translate(30px, 30px)注意：translate``rotate等方法都是需要单位的，而matrix方法e, f参数单位可以省略。

总结：

transform: matrix(xxx, xxx, xxx, xxx, 水平偏移距离, 垂直偏移距离);

缩放，旋转与倾斜

偏移是matrix效果中最简单的，最容易理解的，下面看一下矩阵的缩放，旋转以及倾斜效果。

缩放

上面的示例：

transform: matrix(1, 0, 0, 1, 30, 30);

我们看到，最后那两个值是控制平移的，元素是没有缩放的（ `1: 1`），其中参数中有两个`1`,事实上，这两个就是控制缩放的，由上面的公式可以得到，第一个`1`是控制缩放`x`轴的，第二个`1`是控制`y`轴的。

假设原始点为(x,y)缩放比例为s，则有matrix(s, 0, 0, s, 0, 0)于是套用公式有：

$y^{‘} = bx + dy + f = 0 \times x + s \times y + 0 = {\color{Red} {s \times y}}$
也就是说matrix(s, 0, 0, s, 0, 0)就等同与scale(s, s)。

transform: matrix(0.5, 0, 0, 0.8, 0, 0);

旋转

旋转相比前面两个更要高级些，要用到三角函数。
方法以及参数使用如下：假设角度为θ：

matrix(cosθ, sinθ, -sinθ, cosθ, 0, 0)

结合矩阵公式，就有：

$y^{‘} = x \times \sin \theta + y \times \cos \theta + 0 = x \times \sin \theta + y \times \cos \theta = x \sin \theta + y \cos \theta$

transform: matrix(0.866025,0.500000,-0.500000,0.866025,0,0);
// transform: matrix(cos(30deg), sin(30deg), -sin(30deg), cos(30deg), 0, 0);

倾斜

倾斜也用到了三角函数，不过是tanθ，而且，至于b,c两个参数相关，书写如下（注意y轴倾斜角度在前）：

matrix(1,tan(θy),tan(θx),1,0,0)

结合矩阵公式，就有：

$y^{‘} = x \times \tan {(\theta y)} + y + 0 = x \times \tan {(\theta y)} + y = x \tan {(\theta y)} + y$

transform: matrix(1, 0.57735, 0.57735, 1, 0, 0);
// tan(30deg) = 0.57735

其他效果

既然有简单的skew，rotate等方法，那么matrix有何用？
答：因为他可以实现一些其他的效果，比如“镜像对称”

transform: matrix(-1, 0, 0, 1, 0, 0);

实际上，在镜像对称的时候轴是看不见的。
轴围绕的那个点就是CSS3中transform变换的中心点，自然，镜像对称也不例外。因为该轴永远经过原点，因此，任意对称轴都可以用y = k * x表示。则matrix表示就是：

matrix((1-k*k) / (1+k*k), 2k / (1 + k*k), 2k / (1 + k*k), (k*k - 1) / (1+k*k), 0, 0)

这个如何得到的呢？啊，高中数学来了，就当再高考一次吧，如下图，已经y=kx，并且知道点(x, y)坐标，求其对称点(x’, y’)的坐标？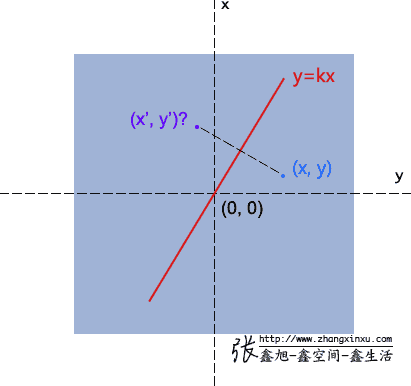

很简单，一是垂直，二是中心点在轴线上，因此有：
$(y-y’) / (x - x’) = -1/ k → ky-ky’ = -x+x’$
$(x + x’) / 2 * k = (y + y’)/2 → kx+kx’ = y+y’$
很简单的，把x'和y'提出来，就有：
$x’ = (1-kk)/(kk+1) x + 2k/(kk+1) y$
$y’ = 2k/(kk+1) x + (kk-1)/(kk+1) y$
在结合矩阵公式：
$x’ = ax+cy+e$
$y’ = bx+dy+f$
我们就可以得到：
$a = (1-kk)/(kk+1);$
$b = 2k/(kk+1);$
$c = 2k/(kk+1);$
$d = (kk-1)/(kk+1);$

3D变换中的矩阵

https://www.zhangxinxu.com/wordpress/2012/09/css3-3d-transform-perspective-animate-transition/
3D变换虽然只比2D多了一个D，但是复杂程度不只多了一个。从二维到三维，是从4到9；而在矩阵里头是从33变成44, 9到16了。
其实，本质上很多东西都与2D一致的，只是复杂度不一样而已。这里就举一个简单的3D缩放变换的例子。
对于3D缩放效果，其矩阵如下：
$\begin{bmatrix}
sx & 0 & 0 & 0\newline
0 & sy & 0 & 0\newline
0 & 0 & sz & 0\newline
0 & 0 & 0 & 1
\end{bmatrix}$
代码表示就是：

transform: matrix3d(sx, 0, 0, 0, 0, sy, 0, 0, 0, 0, sz, 0, 0, 0, 0, 1)