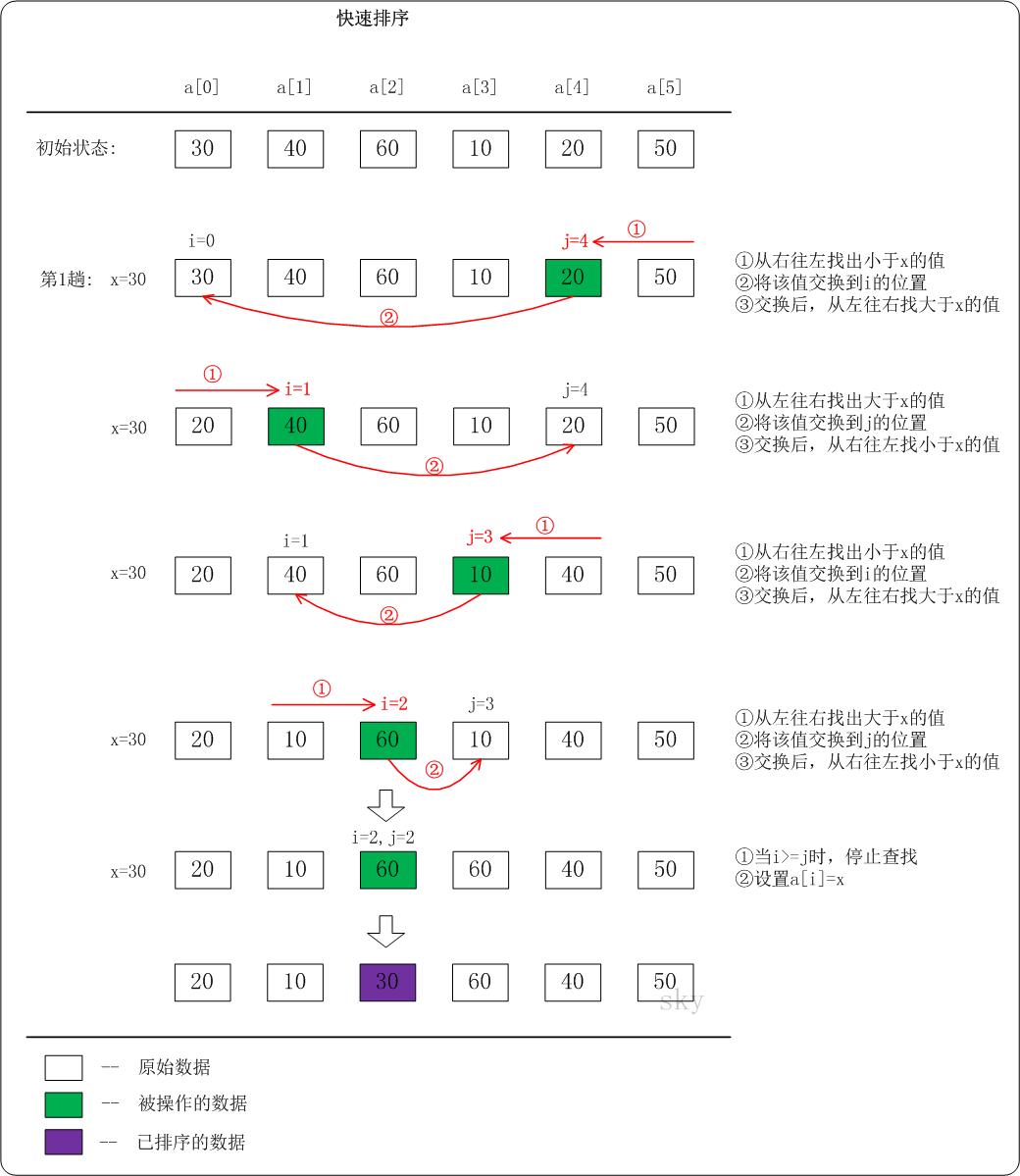
快速排序

快速排序（英语：Quicksort），又称划分交换排序（partition-exchange sort），通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

步骤为：

从数列中挑出一个元素，称为”基准”（pivot），
重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。
递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会结束，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

快速排序的分析

PHP实现快速排序

<?php
function quick_sort(&$nums,$start,$end){
	// 递归集  递归的退出条件
	if($start >= $end){
		return;
	}
	// 设定起始元素为要寻找位置的基准元素
	$mid = $nums[$start];
	// low为序列左边的由左向右移动的游标
	$low = $start;
	// high为序列右边的由右向左的游标
	$high = $end;
	while ($low < $high) {
		// 如果low与high为重合，high指向的元素不比基准小，则low向左移动
		while($low < $high && $nums[$high] >= $mid){
			$high -= 1;
		}
		// 将high指向的元素放到low的位置上
		$nums[$low] = $nums[$high];
		// 如果low与high为重合
		while($low < $high && $nums[$low] < $mid){
			$low += 1;
		}
		// 将low指向的元素放到high的位置上
		$nums[$high] = $nums[$low];
	}
	// 退出循环后，low与high重合，此时所指位置为基准元素的正确位置
	// 将基准元素放到该位置
	$nums[$low] = $mid;
	// 对基准元素左边的子序列进行快速排序
	quick_sort($nums,$start,$low - 1);
	// 对基准元素右边的子序列进行快速排序
	quick_sort($nums,$low + 1,$end);

}
$nums = [4,8,6,7,2,1,9,3];
quick_sort($nums,0,count($nums)-1);
var_dump($nums);

Python实现快速排序

def quick_sort(alist, start, end):
    """快速排序"""

    # 递归的退出条件
    if start >= end:
        return

    # 设定起始元素为要寻找位置的基准元素
    mid = alist[start]

    # low为序列左边的由左向右移动的游标
    low = start

    # high为序列右边的由右向左移动的游标
    high = end

    while low < high:
        # 如果low与high未重合，high指向的元素不比基准元素小，则high向左移动
        while low < high and alist[high] >= mid:
            high -= 1
        # 将high指向的元素放到low的位置上
        alist[low] = alist[high]

        # 如果low与high未重合，low指向的元素比基准元素小，则low向右移动
        while low < high and alist[low] < mid:
            low += 1
        # 将low指向的元素放到high的位置上
        alist[high] = alist[low]

    # 退出循环后，low与high重合，此时所指位置为基准元素的正确位置
    # 将基准元素放到该位置
    alist[low] = mid

    # 对基准元素左边的子序列进行快速排序
    quick_sort(alist, start, low-1)

    # 对基准元素右边的子序列进行快速排序
    quick_sort(alist, low+1, end)

alist = [54,26,93,17,77,31,44,55,20]
quick_sort(alist,0,len(alist)-1)
print(alist)

时间复杂度

最优时间复杂度：O(nlogn)
最坏时间复杂度：O(n^2)
稳定性：不稳定
从一开始快速排序平均需要花费O(nlog n)时间的描述并不明显。但是不难观察到的是分区运算，数组的元素都会在每次循环中走访过一次，使用O(n)的时间。在使用结合（concatenation）的版本中，这项运算也是O(n)。

在最好的情况，每次我们运行一次分区，我们会把一个数列分为两个几近相等的片段。这个意思就是每次递归调用处理一半大小的数列。因此，在到达大小为一的数列前，我们只要作log n次嵌套的调用。这个意思就是调用树的深度是O(log n)。但是在同一层次结构的两个程序调用中，不会处理到原来数列的相同部分；因此，程序调用的每一层次结构总共全部仅需要O(n)的时间（每个调用有某些共同的额外耗费，但是因为在每一层次结构仅仅只有O(n)个调用，这些被归纳在O(n)系数中）。结果是这个算法仅需使用O(nlog n)时间。

快速排序演示